Las metodologías cuantitativas en Psicología, incluyendo la experimental, hacen uso de análisis estadísticos. Se espera que las estudiantes preuniversitarias que realicen un estudio experimental elaboren un análisis de sus datos que incluya estadística descriptiva e inferencial. La estadística descriptiva resume los datos recolectados en un experimento mientras que la estadística inferencial permite sacar conclusiones de los resultados. En un experimento se desea inferir patrones en la muestra que permitan concluir si esos patrones aplican para la población objetivo del estudio.
Objetivos del análisis estadístico:
- Resumir los datos utilizando estadística descriptiva apropiada para el tipo de datos recolectados, incluyendo una medida de tendencia central y una de dispersión.
- Graficar los resultados de manera apropiada, reflejando la hipótesis planteada.
- Sacar una conclusión del experimento realizado mediante el uso de una prueba de estadística inferencial apropiada.
Tanto los datos estadísticos como el gráfico deben tener en cuenta los siguientes elementos:
- Las variables independiente y dependiente (VI y VD)
- La hipótesis experimental, si es de una cola o de dos colas
- La hipótesis nula
- El diseño experimental, si son medidas repetidas o medidas independientes
- El nivel de medición de los de datos recolectados
- Los datos brutos recolectados
Tipos de variables y nivel de medición de los datos:
Las variables que se miden pueden ser continuas o discretas. El tipo de variable va a determinar el nivel de medición de los datos recolectados que pueden ser nominales, ordinales, de intervalo o de razón; es necesario tener claridad sobre el nivel de medición de los datos que se recolectan a partir de los materiales que se diseñan con este fin. El nivel de medición de los datos informa sobre las medidas de estadística descriptiva e inferencial que se puede utilizar para hacer el análisis correspondiente
Variables discretas y continuas:
Algunas variables discretas sólo incluyen unos valores determinados que se representan en datos ordinales o nominales. También incluyen valores numéricos enteros que no son continuos como el número de palabras recordadas en un experimento de memoria; en estos casos los datos pueden ser de intervalo o de razón. Las variables continuas llevan a datos numéricos que se pueden expresar en decimales o fracciones y sus datos pueden ser de intervalo o de razón.
Nivel de medición de los datos:
Los datos nominales no tienen un orden específico, sino que se refieren a una categoría o cualidad que se rotula más que a una cantidad, categorías o cualidades que son mutuamente excluyentes. Para estos datos no se pueden aplicar operaciones aritméticas como suma, resta, multiplicación o división. En los estudios experimentales sencillos la VI es nominal porque representan las condiciones experimentales. La VD puede ser nominal; como cuando se determinan si un participante pudo o no realizar la tarea que se le presentó o cuando se indaga sobre la preferencia entre varias opciones como las preferencias de alimentos. La VD también puede ser de los otros tres niveles de medición que se describen a continuación.
Los datos ordinales se expresan en rangos determinados por un orden. Por ejemplo, las Escalas de Likert que a veces se incluyen en las encuestas se configuran en datos ordinales. También son datos ordinales el orden de llegada en una carrera, aunque la diferencia entre los tiempos de los diferentes competidores varíe. Para estos datos tampoco se pueden aplicar operaciones aritméticas como suma, resta, multiplicación o división.
Los datos de intervalo no sólo informan sobre un orden, sino que además contienen intervalos iguales. Un ejemplo de un dato de intervalo es el coeficiente intelectual (CI). Es posible que exista un cero dentro de la escala, pero no significa que la cualidad esté ausente como es el caso de la temperatura en grados centígrados; existen temperaturas negativas y positivas, pero el cero no significa ausencia de temperatura, sino que es un punto arbitrario en la escala. En este tipo de datos se pueden aplicar las operaciones de suma y resta, pero no las de multiplicación y división.
Los datos de razón además de tener intervalos iguales, también tiene un cero real que evidencia la ausencia de algo. Un ejemplo de este tipo de variables es el tiempo que le toma al participante realizar una tarea o el número de palabras que se recuerdan de una lista. En este tipo de datos se pueden aplicar todas las operaciones aritméticas de suma y resta, multiplicación y división.
El tipo de datos a recolectar va a depender del objetivo de investigación y de la hipótesis que se formule.
Los siguientes videos se pueden ver la diferencia entre los diferentes niveles de medición:
Hipótesis de investigación:
Al interpretar el nivel de significancia estadística en la prueba de estadística inferencial es importante tener en cuenta si la hipótesis planteada es de una cola, es decir que señala una dirección en los resultados, o de dos colas, en que sólo se postula que va a haber una diferencia entre los grupos. Recordemos que la hipótesis experimental consiste en una afirmación de lo que se espera hallar como resultado del experimento que la pone a prueba; propone cómo la VI va a afectar la VD.
Hipótesis nula:
La hipótesis nula es una afirmación que expresa que no hay ninguna relación entre a VI y la VD. Esta es la hipótesis que se busca descartar por medio del experimento. El análisis de estadística inferencial busca rechazar la validez de esta hipótesis.
Diseños experimentales:
La decisión del tipo de estadística descriptiva e inferencial que se decida utilizar depende no sólo del nivel de medición de los datos sino también del diseño experimental que se implemente en el estudio. Se pueden utilizar uno de los siguientes tres diseños experimentales:
- Diseño de muestras independientes (entre grupos) – En este tipo de diseño los participantes se dividen en grupos, uno para cada condición de la VI.
- Diseño de medidas repetidas (intragrupo) – En este tipo de diseño todos los participantes experimentan todas las condiciones de la VI
- Diseño pareado – Se hace una evaluación previa en una variable o más variables importantes como sería la capacidad de memoria y se forman grupos en que cada participante de un grupo se aparea con uno de otro grupo.
Nota – Para más información de los diseños experimentales ver artículo sobre “Estudios Experimentales Controlados en Psicología.”
Tablas de datos:
Distribución normal de los datos:
Una vez se hayan recogido los datos se debe hacer una tabla con ellos e incluirla en los apéndices. Esta tabla también tiene como objetivo organizar los datos con el fin de hacer el análisis estadístico. Los encabezados de las columnas de la tabla representan la VI mientras que las filas proveen los datos de la VD por participante. La tabla que se haga permitirá también localizar los datos anómalos, es decir, aquellos que difieren de manera significativa de los demás datos recolectados. Los datos anómalos pueden afectar los resultados y se puede decidir no incluirlos en el análisis estadístico.
Este es un ejemplo de tabla de datos brutos que debe incluírse en los apéndices
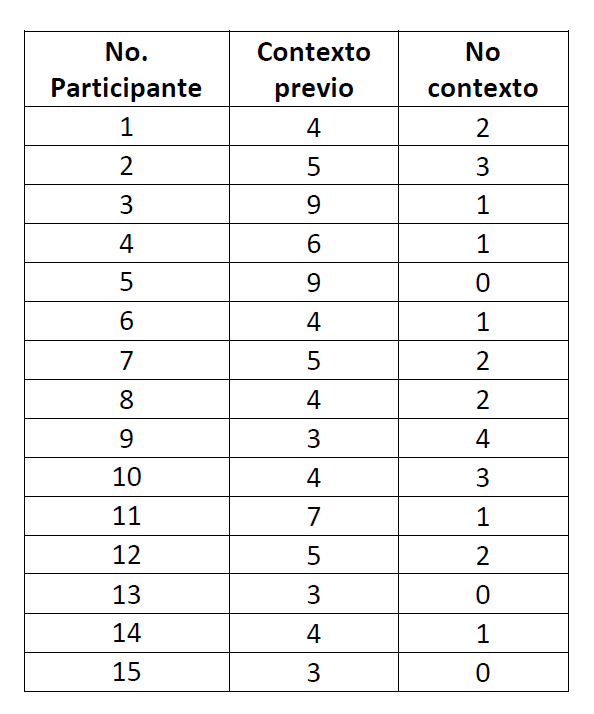
Cuando los datos recolectados son de intervalo o de razón es importante ver si éstos reflejan una distribución normal porque de ello depende si se puede realizar una prueba paramétrica o si hay que calcular una no-paramétrica. Una distribución normal es aquella que se refleja en una campana de Gauss. Aunque muchas variables reflejan esta distribución en la población, cuando se hace un estudio experimental con pocas participantes como los que hacen estudiantes preuniversitarias, es muy probable que los datos recolectados no reflejen este tipo de distribución y por lo tanto se requiera calcular una prueba no-paramétrica de estadística inferencial. Es posible que entre los datos existan valores atípicos que sean muy distintos a los demás datos; en estos casos es muy probable que la distribución no sea normal.
Medidas de estadística descriptiva:
La estadística descriptiva, como su nombre lo dice, describe patrones en los datos que se han recolectado y los resumen. Existen dos tipos de medidas de estadística descriptiva: Medidas de tendencia central y medidas de dispersión. El tipo de medidas de estadística descriptiva a utilizar dependen del nivel de medición de los datos de la VD y de la distribución de éstos. Este tipo de estadística se puede calcular utilizando una hoja de cálculo como Excel o una aplicación estadística en línea.
Medidas de tendencia central:
Las medidas de tendencia central son diferentes maneras de presentar el promedio de los datos recolectados. En otras palabras, reflejan el valor más típico de un conjunto de datos numéricos.
Existen tres tipos de medidas de tendencia central y su uso puede depender del nivel de medición de los datos recolectados:
- Moda – Este es el valor que se presenta con mayor frecuencia en los datos recolectados. Esta es la medida a reportar cuando se recogen datos nominales que no son numéricos y sólo miden la frecuencia de cada opción dada para la VD. Por ejemplo, si se mira cuando se logra o no realizar la tarea, la moda sería el número de personas con mayor frecuencia en una de estas dos opciones.
- Mediana – Este es el valor que aparece en el medio de los valores recolectados. Esta es la medida que preferiblemente se reporte cuando se recogen datos ordinales, aunque en el caso de datos ordinales también es posible reportar la moda. Para encontrar la mediana se ordenan los datos para encontrar el que se encuentra en la mitad. Cuando la mediana se encuentre entre dos datos diferentes, lo cual puede ocurrir cuando la cantidad de datos es par, estos se suman y el resultado se divide por dos. También se utiliza cuando hay datos atípicos que reflejen grandes desviaciones en la distribución de los datos de intervalo o de razón que afecten la media.
- Media – Esta es el promedio aritmético y se encuentra sumando todos los datos para luego dividir por la cantidad de datos recogidos. Esta es la medida a utilizar cuando se recolectan datos de intervalo o de razón. Sin embargo, en el caso que se presente uno o más datos anómalos, atípicos o extremos, ya sean datos muy altos o bajos, que no se quieren descartar pero que pueden afectar la validez de la media, entonces se puede utilizar la mediana como medida de tendencia central. De igual manera, si el patrón de distribución de los datos es anormal, también es mejor utilizar la mediana en vez de la media. En una distribución normal la media, la mediana y la moda deben ser iguales o muy similares.
Cuando la distribución de los datos refleja una curva normal, la moda, la mediana y la media coinciden. En caso contrario, especialmente cuando hay datos atípicos, son diferentes, lo cual se debe tener en cuenta al escoger la medida de tendencia central a utilizar.
Al interpretar la media y la mediana, es necesario tener en cuenta la variabilidad de los datos utilizando una medida de dispersión.
Medidas de dispersión:
Los datos recolectados pueden estar dispersos en mayor o menor medida. Las medidas de dispersión muestran cómo varían los datos de una variable; un grupo de datos puede estar más disperso que los otros. Además de reportar una medida de tendencia central (promedio), un investigador también debe reportar la variabilidad de los datos que está describiendo.
Existen cuatro tipos de medidas de dispersión y su uso depende del nivel de medición de los datos recolectados, si son ordinales, de intervalo o de razón. En el caso de los datos nominales no se utiliza una medida de dispersión.
- Rango – Esta es la diferencia entre el valor más alto y el más bajo de un conjunto de datos. La limitación de esta medida es que se distorsiona de manera significativa cuando hay datos atípicos.
- Rango intercuartílico o intercuartil – Esta es una medida que representa el rango del 50% central de los valores. Cuando los datos recolectados son ordinales, se debe reportar el rango intercuartílico, también llamado rango intercuartil. La mediana sería el segundo intercuartil, dividiendo los resultados de la muestra por la mitad, de tal manera que el 50% de los datos se encuentran por debajo de la mediana y el otro 50% serían mayores a la mediana. El primer intercuartil (Q1) divide la mitad inferior de los datos de tal manera que el 25% de los datos están por debajo de este valor y el 75% restante serían más altos. El tercer intercuartil (Q3) es la medida que separa el 25% de los datos más altos del resto. El rango intercuartílico sería la diferencia entre el tercer intercuartil y el primer intercuartil (Q3 – Q1), representando el 50% de los valores centrales. Esta medida, contrario a la desviación estándar, no asume una distribución normal de los datos. El siguiente video explica cómo encontrar tanto la mediana como el rango intercuartil:
Si el rango intercuartil de un grupo de datos es menor que lel del otro, quiere decir que estos datos están menos dispersos y más cercanos a la mediana. Al contrario, si la el rango intercuartil es alto, los datos están más dispersos y alejados de la mediana.
También se puede utilizar el rango semi-intercuartil, que se calcula dividiendo por dos el rango intercuartil; en otras palabras, es la mitad de la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1), obtenido utilizando la siguiente fórmula: (Q3 – Q1)/2.
La ventaja del rango semi-intercuartil es que se afecta poco por los datos atípicos y por lo tanto es una buena medida de dispersión cuando los datos son sesgados.
- Varianza – Esta medida muestra el grado en que los datos difieren de la media, teniendo en cuenta todo el conjunto de datos y sólo se puede utilizar cuando el nivel de los datos es de intervalo o de razón.
- Desviación estándar – Esta es una buena medida de dispersión que tiene en cuenta todos los datos, utiliza toda la información disponible y muestra en promedio qué tanto los datos difieren de la media. La desviación estándar es la raíz cuadrada de la varianza y es la medida de dispersión que se utiliza con mayor frecuencia cuando el nivel de los datos es de intervalo o de razón y se ha utilizado la media como medida de tendencia central. Sin embargo, en el caso que se presenten uno o más datos anómalos o extremos que no se quieren descartar pero que pueden afectar la desviación estándar, entonces se puede utilizar el rango intercuartílico, también llamado rango intercuartil.
Si la desviación estándar de un grupo de datos es menor que la otra, quiere decir que estos datos están menos dispersos y más cercanos a la media. Al contrario, si la desviación estándar es alta, los datos están más dispersos y alejados de la media.
Los datos de la estadística inferencial se deben interpretar teniendo en cuenta los datos y no se pueden utilizar para sacar conclusiones sobre las hipótesis, como se muestra en el siguiente ejemplo:
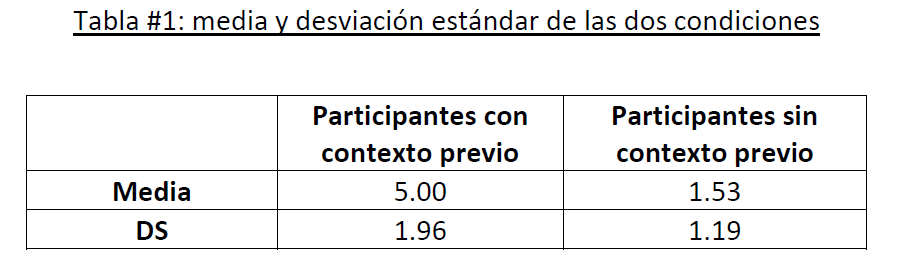
El experimento recolectó datos de razón, sin presentar datos atípicos, lo que permitió calcular la media y la desviación estándar. De la Tabla #1 por las medias se puede deducir que la condición de contexto (Media = 5,00) tuvo una mayor recuperación de ideas del texto, mientras la de no contexto (Media = 1,53) una menor recuperación, indicando el efecto de las condiciones sobre la variable dependiente. Al analizar las desviaciones estándar (1,96 y 1,19) se puede inferir que los datos de la condición de contexto previo tuvieron resultados más dispersos que los de la condición de no contexto.
El siguiente video informa sobre aspectos relacionados con la estadística descriptiva:
Gráfica de los datos:
En los estudios experimentales que realizan estudiantes preuniversitarias, por lo general la gráfica más apropiada a utilizar es una de barras. El gráfico es una representación de la estadística descriptiva, principalmente de la medida de tendencia central calculada para los datos recogidos durante el experimento. Para representar la variabilidad de los datos (ej. desviación estándar), se pueden incluir barras de error, aunque éstas no son requeridas. Un gráfico de barras apropiado muestra de manera rápida y clara los resultados del estudio. Es importante que el gráfico aborde la hipótesis de investigación. Estas gráficas se pueden hacer utilizando una hoja de cálculo como Excel.
A continuación, se enumeran algunos aspectos que se deben tener en cuenta al hacer el gráfico:
- El gráfico debe estar conectado de manera clara con la hipótesis, incluyendo la información relevante y un título claro.
- los ejes deben estar rotulados de tal manera que el eje X refleje la VI y sus condiciones y el eje Y la VD que se ha medido, evitando el uso de rótulos vagos como Grupo 1 y Grupo 2.
- Las unidades de medición deben estar incluidas en el rótulo del eje Y.
- La numeración del eje Y debe iniciare en cero para que no se observe distorsión en las barras.
- La gráfica de barras refleja de manera visual las medidas de estadística descriptiva que se reporten.

Uso de prueba de estadística inferencial para determinar niveles de significancia:
Con el fin de sustentar una hipótesis de investigación es necesario utilizar una prueba de estadística inferencial y de esta manera llegar a conclusiones del estudio. Se trata de encontrar si los resultados son significativos utilizando una prueba apropiada de estadística inferencial. El nivel de significancia de las diferentes condiciones de la VI en un experimento no se pueden determinar por las diferencias en las medidas de estadística descriptiva, es decir por diferencias observadas en la medida de tendencia central utilizada (moda, mediana o media) o por la medida de dispersión (rango intercuartílico o desviación estándar).
Sólo una prueba apropiada de estadística inferencial puede llevar a determinar si la diferencia entre las condiciones experimentales es suficientemente grande de tal manera que no se deba al azar sino a la manipulación de la VI. Así se puede llegar a la conclusión de descartar o no la hipótesis nula porque mediante el uso de esta prueba el investigador puede estar bastante seguro si la hipótesis nula es falsa. Si se puede descartar la hipótesis nula, entonces se sustenta la hipótesis de investigación que postula una diferencia en la VD como resultado de la manipulación de la VI. Si la prueba de estadística inferencial evidencia que la diferencia entre los grupos es significativa con un nivel de seguridad de al menos un 95%, entonces se descarta la hipótesis nula y se sustenta la hipótesis de investigación, así como la teoría siendo puesta a prueba mediante el experimento. En caso de que no se pueda descartar la hipótesis nula porque el resultado de la prueba de estadística inferencial no evidencia una diferencia significativa, se rechazaría la hipótesis de investigación. Sin embargo, esto no significa que la hipótesis de investigación es falsa, sino que no se puede asegurar que sea verdadera.
Al poner a prueba una hipótesis se puede llegar a uno de dos tipos de error. El error tipo I o “falso positivo” ocurre cuando después de hacer un análisis de estadística inferencial se rechaza la hipótesis nula cuando debía ser aceptada, evidenciando un efecto que no es real y sustentando una hipótesis de investigación de manera incorrecta. Esto puede suceder porque una prueba estadística no requiere de un 100% de certeza para rechazar una hipótesis nula sino sólo del 95% y por lo tanto existe la posibilidad de un 5% de tener un falso positivo o error tipo I.
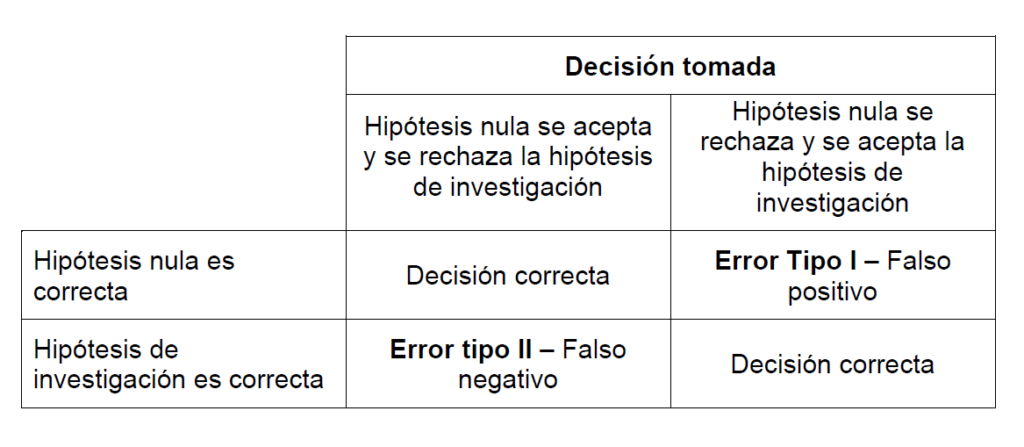
El error de tipo II o “falso negativo” ocurre cuando se acepta la hipótesis nula de manera incorrecta, así rechazando la hipótesis de investigación de manera inapropiada, concluyendo que no existe un efecto que sí existe. Puede ocurrir que la prueba estadística puede estar cerca del nivel de significancia, refutando una hipótesis nula que debió haber sido aceptada, llevando a la aceptación errónea de la hipótesis de investigación, es decir, a un error tipo I o falso positivo.
Para decidir la prueba a utilizar es importante determinar si los datos reflejan una distribución normal. Una distribución expresa la frecuencia de cada resultado en un grupo de datos. La distribución normal que se refleja en lo que se conoce como campana de Gauss tiene tres propiedades: Tiene una forma simétrica y la media, mediana y moda son equivalentes. Adicionalmente, en este tipo de distribución, el 95% de los datos se encuentran entre dos desviaciones estándar por debajo de la media y dos desviaciones estándar por encima de la media. Es raro que un experimento que recoja datos de pocos participantes replique una distribución normal de manera perfecta, aunque muchas de las variables que se miden la reflejen en la vida real.
El siguiente video explica la distribución normal:
Existen dos tipos de pruebas estadísticas, las paramétricas y las no-paramétricas. Para utilizar pruebas paramétricas es importante que los datos reflejen una distribución normal y que el nivel de medición de los datos de la VD sea al menos de intervalo. Si estos requisitos no se cumplen, entonces se tendría que usar una prueba no-paramétrica para no incurrir en un error tipo I. En general, por lo tanto, el tipo de prueba de estadística inferencial a aplicar va a depender del nivel de medición de los datos recolectados para la VD, del diseño experimental utilizado y de si se han cumplido o no los supuestos para una distribución normal en caso de datos de intervalo o razón:
- Pruebas para datos nominales u ordinales:
- Cuando el diseño experimental es de muestras independientes, la prueba a aplicar sería el Chi Cuadrado. Esta prueba compara los datos observados con los números que se esperarían en caso de que la hipótesis nula se aceptara. En caso de que exista una diferencia entre los datos recolectados y los esperados, se puede concluir que hay una diferencia significativa. Al utilizar el Chi cuadrado, se obtiene un valor de p que se puede interpretar de la misma manera como se describe más adelante para la Prueba T.
- Cuando el diseño experimental es de medidas repetidas o muestras pareadas con dos condiciones, la pruebas aplicar serían la Prueba de Signos o la Prueba de McNemar.
- Si los datos son ordinales, la prueba que más se recomienda aplicar es una prueba no-paramétrica que va a depender del diseño experimental.
- En caso de que el diseño experimental sea de medidas repetidas se recomienda aplicar la Prueba de Rangos de Wilcoxon o la Prueba de Friedman en caso de contar con más de dos condiciones de la VI.
- En caso de que el diseño experimental sea de muestras independientes se recomienda aplicar la Prueba U de Mann-Whitney o la Prueba de Kruskal-Wallis en caso de contar con más de dos condiciones de la VI.
- Estas pruebas funcionan estableciendo los rangos de todos los datos y luego comparando las medias de los rangos. Los resultados proveen el valor de la prueba (U para la prueba de Mann-Whitney y W para la de Wilcoxon) y el valor de p, el cual se interpreta de manera similar a como se describe más adelante para la Prueba T.
- Si los datos son de intervalo o de razón se podría aplicar la Prueba T o el ANOVA en caso de contar con más de dos condiciones de la VI. Existen dos tipos de Prueba T, una para muestras independientes, no relacionadas, y otra para muestras relacionadas (medidas repetidas o muestras pareadas). Al utilizar una Prueba T hay que tener en cuenta los siguientes aspectos:
- Los grados de libertad: Este es un número que equivale al número de participantes menos el número de grupos o condiciones experimentales.
- El valor de t: A un mayor valor de t, es más probable que las dos condiciones experimentales sean significativamente diferentes.
- El valor de p: Un valor de p se mide entre 0 y 1 e informa el nivel de confianza que se tiene para rechazar la hipótesis nula. Si el valor de p es suficientemente pequeño, generalmente menor al 0,05, el investigador puede estar bastante seguro de rechazar la hipótesis nula. Un valor de p de 0,05 significa que existe una probabilidad de que el 95% de los resultados reflejan una diferencia significativa.
Estas pruebas se llaman paramétricas porque para calcularlas utilizan parámetros como la media y la desviación estándar y por lo tanto asumen que los datos reflejen una distribución normal. Por ese motivo, antes de utilizar una prueba paramétrica es necesario utilizar una prueba como la Prueba de Normalidad de Shapiro-Wilk para determinar la normalidad de los datos.
En caso de que los datos no reflejen una distribución normal, lo cual es común cuando se usan muestras pequeñas como las de los estudios experimentales que realizan estudiantes preuniversitarias, entonces se tendría que utilizar una prueba no-paramétrica como las enumeradas para los datos ordinales. Igualmente, si no hay homogeneidad de la varianza, es decir que la desviación estándar de los datos entre las condiciones es muy distinta, no se recomienda utilizar una prueba paramétrica, prefiriendo el uso de una prueba no-paramétrica. Las pruebas no-paramétricas no utilizan la media y la desviación estándar para calcularlas. En estos casos, los datos de intervalo y de razón se deben convertir en datos ordinales.
Las estudiantes no tienen que hacer sus propios cálculos estadísticos tanto descriptivos como inferenciales; estos los pueden hacer utilizando una hoja de cálculo como Excel y Google Sheets o una aplicación en línea como Vassarstats o Social Science Statistics. Sin embargo, es importante que tengan claridad sobre cuáles utilizar y cómo interpretarlos. Aun así, tener claridad sobre las fórmulas que se utilizan para calcularlos puede dar más información sobre la manera de interpretarlos.
Al reportar los resultados de la prueba de estadística inferencial, es importante indicar si se encontró una diferencia estadística significativa entre los grupos, teniendo en cuenta si la hipótesis planteada es de una cola o de dos colas. Se debe reportar el valor numérico de la prueba estadística, indicando su nivel de probabilidad (p). Un valor de p menor al 0,05 (p<0,05) indica que la probabilidad de que las diferencias en la VD no se deben a las condiciones de la VI es menor al 5%. De esta manera, se puede descartar la hipótesis nula y aceptar la hipótesis de investigación. En otras palabras, la probabilidad de que los resultados sustenten la hipótesis de investigación que postula una diferencia significativa entre las condiciones experimentales es mayor al 95%. En caso de que p sea mayor al 0,05 (p>0,05) se tendría que aceptar la hipótesis nula y descartar la de investigación porque evidencia que los resultados muy probablemente no se deben a las condiciones de la VI. Por ejemplo, un reporte podría ser el siguiente:
Al utilizar la prueba U de Mann-Whitney, se halló una diferencia significativa entre la condición en la que se dio un contexto previo y la condición a la que no se le dio un contexto previo; valor U de Mann-Whitney = 8,5; p < 0,05. Este valor de U es menor al límite inferior de 72 para una prueba de una cola. Por lo tanto, se puede rechazar la hipótesis nula y aceptar la hipótesis de investigación, indicando que los participantes a quienes se les dio un contexto previo lograron recordar un número significativo mayor de ideas del texto que aquellos a los que no se les dio un contexto previo.
El video a continuación ilustra aspectos relacionados con la estadística inferencial:
Bibliografía:
Bryan, C., Giddens, P. & Halkiopoulos, C. (2018). Psychology for the IB Diploma (2nd Edition). London: Pearson Education.
Hernández-Sampieri, R. y Mendoza-Torres, S.P. (2018) Metodología de la investigación: Las rutas cuantitativa, cualitativa y mixta. México: McGraw Hill.
Lawton, J.M. & Willard, E. (2018) Psychology for the IB Diploma (2nd Edition). London: Hodder Education.
Organización del Bachillerato Internacional (2017) Guía de Psicología. Ginebra, Suiza: IBO.
Organización del Bachillerato Internacional (2017) Material de ayuda al profesor de Psicología. Ginebra, Suiza: IBO.
Popov, A., Parker, L. & Seath, D. (2017) IB Psychology course companion (2nd Edition). Oxford: Oxford University Press.

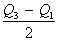
excelente informacion que vierten en el articulo, sintetizada y objetiva.